A. BILANGAN REAL
1. Pengertian Sistem Bilangan Real
Sistem bilangan real adalah himpunan bilangan real R yang disertai dengan operasi penjumlahan dan perkalian sehingga memenuhi aksioma tertentu, dinotasikan dengan : “ ( R , + , x )”. Bilangan real adalah bilangan yang merupakan gabungan dari bilangan rasional dan bilangan irasional. Bilangan real yang dilengkapi dengan sifat – sifat bilangan disebut sistem bilangan real. Dalam aplikasinya himpunan bilangan ini mempunyai banyak turunan yang mempunyai bermacam-macam sifat dan bentuk bilangan.
2. Operasi pada Bilangan Real
Operasi penjumlahan, pengurangan, perkalian, dan pembagian.
a. Operasi penjumlahan
Contoh:
1). 4 + 6 = 10
2). 4 + (-6 ) = -2
b. Operasi pengurangan
Contoh:
1). -6 – 4 = -6 + (-4) = -10
2). 3 -6 – 4 = -6 + (-4) = -10
c. Operasi perkalian
Contoh:
1). 6 x 4 = 24
2). 6 x (-4) = -24
3). (-6) x (-4) = 24
d. Operasi pembagian
Contoh:
1). 12 : 2 = 6
2). 12 : -2 = -6
3). (-12) : (-2) = 6
3. Macam-macam Bilangan Real
a. Bilangan Rasional (Rational Numbers)
Bilangan rasional adalah bilangan yang dapat dinyatakan dalam bentuk a/b dengan a, b bilangan bulat dan b ≠ 0. Bilangan rasional terdiri dari :- Bilangan asli = 1, 2, 3, 4 , 5, …
- Bilangan cacah = 0,1,2,3,…
- Bilangan bulat = -3, -2, -1,0,1,2,3,…
Bilangan bulat dibagi menjadi tiga bagian, yaitu bilangan bulat negatif, bilangan bulat positif, bilangan bulat nol.
Bilangan pecahan dapat dibagi menjadi dua bagian, yaitu pecahan biasa dan pecahan campuran.
b. Bilangan Irasional (Irrational Numbers)
b. Bilangan Irasional (Irrational Numbers)
Dalam matematika, bilangan irasional adalah bilangan real yang tidak bisa dibagi (hasil baginya tidak pernah berhenti). Dalam hal ini, bilangan irasional tidak bisa dinyatakan sebagai a/b, dengan a dan b sebagai bilangan bulat dan b tidak sama dengan nol.
Contoh bilangan irasional √3 = 1,732050807 yang ternyata tidak mempunyai pola berulang secara teratur, dan tidak akan berakhir bilangan √3 merupakan salah satu contoh bilangan irasional.
B. HIMPUNAN
1. Pengertian Himpunan
Himpunan adalah suatu daftar, koleksi atau kelas objek-objek yang mempunyai sifat atau ciri-ciri tertentu. Objek dalam suatu himpunan dapat berupa bilangan, orang, kota, dan lain sebagainya yang memiliki sifat atau ciri-ciri yang sama. Sifat tersebut berguna untuk membedakan apakah suatu objek itu meupakan anggota himpunan tersebut atau bukan. Pada umumnya himpunan ditulis dengan huruf besar (A, B, C, D,.....) dan anggota himpunan ditulis dengan huruf kecil (a, b, c, d,...).
Himpunan ditulis diantara dua kurung {.....} dan dapat disajikan dengan 2 cara yaitu:
- Mendaftarkan anggota-anggotanya; dan
- Menyatakan sifat anggota-anggotanya.
Contoh:
Himpunan A = {1, 2, 3, 4, 5, 6, 7, 8, 9}.
Banyak anggota himpunan A = n(A) = 9
Himpunan memiliki anggota yang terhingga atau tak terhingga. Himpunan dengan banyak anggota terhingga atau dibatasi sampai batas tertentu disebut himpunan berhingga. Sedangkan, himpunan dengan banyak anggota tak terbatas adalah himpunan tak berhingga.
Contoh:
Himpunan berhingga: {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
Himpunan tak berhingga: {25, 27, 29, 31, …}
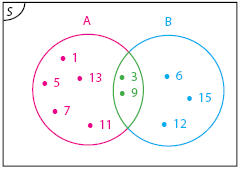
Diagram Venn
Diagram venn adalah gambar himpunan yang digunakan untuk menyatakan hubungan beberapa himpunan.
2. Macam-macam Himpunan
Himpunan berhingga: {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
Himpunan tak berhingga: {25, 27, 29, 31, …}
Diagram Venn
Diagram venn adalah gambar himpunan yang digunakan untuk menyatakan hubungan beberapa himpunan.
2. Macam-macam Himpunan
- Himpunan Semesta
- Himpunan Bagian
Rumus mencari banyaknya himpunan bagian.
Himpunan = A
Banyak anggota himpunan A = n(A)
Banyaknya himpunan bagian A adalah
Contoh:Himpunan = A
Banyak anggota himpunan A = n(A)
Banyaknya himpunan bagian A adalah
B = {1, 2, 3}
n(B) = 3
Banyaknya himpunan bagian B adalah  yaitu { }; {1}; {2}; {3}; {1, 2}; {1, 3}; {2, 3}; {1, 2, 3}.
yaitu { }; {1}; {2}; {3}; {1, 2}; {1, 3}; {2, 3}; {1, 2, 3}.
 b. Gabungan
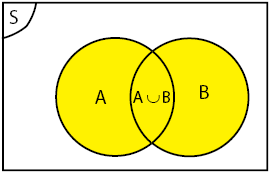
b. Gabungan
Gabungan dua himpunan A dan B adalah himpunan yang anggota-anggotanya merupakan anggota himpunan A atau anggota himpunan B.

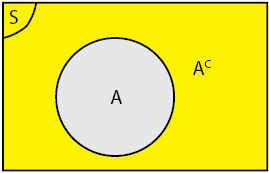
 adalah himpunan yang anggota-anggotanya merupakan anggota himpunan semesta namun bukan anggota himpunan A.
adalah himpunan yang anggota-anggotanya merupakan anggota himpunan semesta namun bukan anggota himpunan A.


4. Sifat-Sifat Operasi Himpunan
Pembahasan dalam materi himpunan dan diagram venn yang tidak kalah penting untuk dibahasa adalah sifa-sifat operasi pada himpunan. Sifat-sifat operasi himpunan meliputi komutatif, asosiatif, ditributif, dan dalil de Morgan.
a. Komutatif


b. Asosiatif


c. Distributif


d. Dalil de Morgan


- Himpunan Kosong
Himpunan kosong adalah himpunan yang tidak mempunyai anggota. Himpunan kosong akan selalu menjadi himpunan bagian dari anggota himpunan bagian. Notasi himpunan kosong adalah { }.
3. Hubungan Antar Himpunan
Hubungan antarhimpunan meliputi irisan, gabungan, komplemen himpunan, dan selisih himpunan. Lebih lanjut mengenai keempatnya dapat dilihat seperti pembahasan di bawah.
Hubungan antarhimpunan meliputi irisan, gabungan, komplemen himpunan, dan selisih himpunan. Lebih lanjut mengenai keempatnya dapat dilihat seperti pembahasan di bawah.
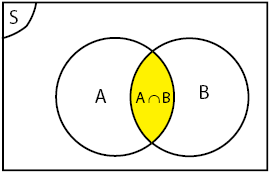
a. Irisan
Irisan dua himpunan A dan B adalah himpunan yang anggota-anggotanya merupakan anggota A dan anggota B.
Irisan dua himpunan A dan B adalah himpunan yang anggota-anggotanya merupakan anggota A dan anggota B.

Gabungan dua himpunan A dan B adalah himpunan yang anggota-anggotanya merupakan anggota himpunan A atau anggota himpunan B.

c. Komplemen

d. Selisih
A − B adalah himpunan yang anggota-anggotanya merupakan anggota himpunan A namun bukan anggota himpunan B.

A − B adalah himpunan yang anggota-anggotanya merupakan anggota himpunan A namun bukan anggota himpunan B.

4. Sifat-Sifat Operasi Himpunan
Pembahasan dalam materi himpunan dan diagram venn yang tidak kalah penting untuk dibahasa adalah sifa-sifat operasi pada himpunan. Sifat-sifat operasi himpunan meliputi komutatif, asosiatif, ditributif, dan dalil de Morgan.
a. Komutatif
b. Asosiatif
c. Distributif
d. Dalil de Morgan
(N)
Tidak ada komentar:
Posting Komentar