Rabu, 10 Oktober 2018

LIMIT FUNGSI

A. Definisi Limit Fungsi
Limit suatu fungsi merupakan salah satu konsep mendasar dalam kalkulus dan analisis, tentang kelakuan suatu fungsi mendekati titik masukan tertentu. Kata limit identik dengan kata mendekati atau hampiran. Lebih lengkap secara matematika limit diartikan sebagai nilai yang mendekati sebuah variabel bilangan real. Limit fungsi dapat diartikan sebagai nilai pendekatan suatu fungsi ketika variabelnya mendekati atau menuju suatu bilangan tertentu. 

Suatu fungsi memetakan keluaran f(x) untuk setiap masukan x. Fungsi tersebut memiliki limit L pada titik masukan p bila f(x) "dekat" pada L ketika x dekat pada p. Dengan kata lain, f(x) menjadi semakin dekat kepada L ketika x juga mendekat menuju p. Lebih jauh lagi, bila f diterapkan pada tiap masukan yang cukup dekat pada p, hasilnya adalah keluaran yang (secara sembarang) dekat dengan L. Bila masukan yang dekat pada p ternyata dipetakan pada keluaran yang sangat berbeda, fungsi f dikatakan tidak memiliki limit.

B. Cara Membaca Notasi Limit


Notasi atau penulisan limit dalam matematika dikenal sebagai berikut,
Lalu apa arti notasi limit di atas? Sebelumnya anda harus tahu bagaimana cara membaca notasi limit di atas. Notasi di atas dibaca " Limit fungsi f(x) untuk x mendekati a sama dengan K".
Jika dimisalkan f adalah fungsi dan K adalah bilangan Real, maka  jika dan hanya jika f(x) mendekati K untuk semua x yang mendekati a.


C. Teknik-Teknik Untuk Menyelesaikan Limit
Ada beberapa bentuk limit jika diselesaikan dengan suatu metode akan menghasilkan nilai \frac{0}{0}. Sebagian besar, banyak yang menganggap bahwa ini adalah hasil akhir nilainya. Padahal, pada beberapa kasus, bentuk \frac{0}{0} bukan merupakan nilai limit. Diperlukan metode yang tepat untuk menentukan nilai limit fungsi di suatu titik. Ada tujuh cara dalam menyelesaikan limit, yaitu :

1. Substitusi nilai limit x pada persamaan

Cara pertama yang perlu dilakukan untuk mengetahui suatu nilai limit fungsi adalah dengan melakukan substitusi nilai limit x pada persamaan. Jika hasil yang diperoleh adalah suatu nilai, (bukan \frac{0}{0}) maka proses mencari nilai limit berhenti sampai di sini. Untuk lebih jelasnya, perhatikan contoh cara mencari nilai limit di bawah.
  \[ \lim_{x \rightarrow 4} \frac{x^{2} - 2x - 3}{x^{2} - 9} \]
Untuk mendapatkan nilai limit fungsi seperti bentuk di atas, perlu melakukan substitusi nilai x = 4 pada persamaan fungsinya.
  \[ \lim_{x \rightarrow 4} \frac{x^{2} - 2x - 3}{x^{2} - 9} = \frac{4^{2} - 2 \cdot 4 - 3}{4^{2} - 9} \]
  \[ = \frac{16 - 8 - 3}{16 - 9} \]
  \[ = \frac{5}{7} \]
Proses mencari nilai limit sudah berakhir di sini.
Bentuk limit fungsi yang dapat diselesaikan menggunakan substitusi nilai limit x adalah persamaan polinomial, fungsi konstanta, dan bentuk akar nilai positif, dan bentuk pangkat.
Bentuk limit fungsi yang dapat diselesaikan menggunakan cara substitusi:
  \[ \lim_{x \rightarrow 2} 4x = 8 \]
  \[ \lim_{x \rightarrow 1} x^{2} + 3x + 5 = 9 \]
  \[ \lim_{x \rightarrow -1} \left( x + 2 \right)^{100} = 1^{100} = 1 \]
  \[ \lim_{x \rightarrow 0} \sqrt{9 - x^{2}} = \sqrt{9 - 0} = \sqrt{9} = 3 \]
2. Pemfaktoran
Tips kedua yang dapat digunakan untuk menemukan nilai limit adalah metode pemfaktoran. Cara ini digunakan jika proses pencarian nilai limit dengan metode substitusi menghasilkan nilai \frac{0}{0}. Seperti terlihat pada contoh di bawah.
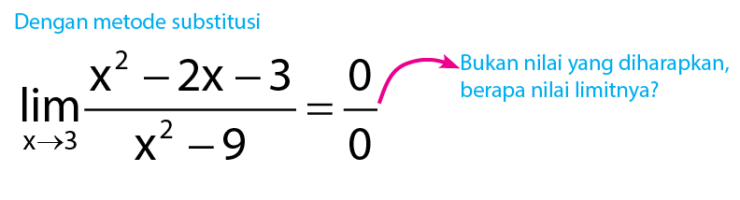
mencari nilai limit fungsi metode pemfaktoran
Hasil limit seperti di atas bukan merupakan nilai limit yang diharapkan. Proses mencari nilai limit belum selesai, untuk mencari nilai limit dengan bentuk ini dapat menggunakan metode pemfaktoran. Perhatikan cara mencari nilai limit dengan metode pemfaktoran yang akan diberikan di bawah.
Mencari Nilai Limit Fungsi Metode Pemfaktoran
Nilai limit di atas merupakan nilai yang diharapkan. Sekarang, perhatikan bentuk limit fungsi yang diberikan di bawah.
mencari nilai imit fungsi metode pemfaktoran
Tidak semua bentuk limit fungsi yang diselesaikan menggunakan pemfaktoran akan menghasilkan nilai limitnya. Pada kasus tertentu, ada bentuk limit fungsi yang tidak memiliki nilai limit fungsi. Beberapa contoh nilai limit fungsi yang tidak memiliki nilai dapat disimak berikut.
Nilai limit fungsi tidak ada
3. Mengalikan dengan Penyebut yang Sama
Metode untuk menentukan nilai limit yang ke tiga adalah mengalikan dengan penyebut. Perhatikan bentuk limit yang diberikan pada persamaan di bawah!Nilai limit fungsi metode penyebut yang samaPenyelesaian bentuk limit di atas menggunakan metode substitusi menghasilkan nilai \frac{0}{0}. Sedangkan metode pemfaktoran juga tidak dapat digunakan karena tidak ada bentuk yang bisa difaktorkan. Sehingga, untuk mendapatkan nilai limit fungsi bentuk ini diperlukan metode lain, yaitu metode mengalikan dengan penyebut yang sama.
Bentuk limit di atas dapat diselesaikan dengan cara mengalikan dengan pembilangnya. Proses menentukan nilai limit dengan metode mengalikan dengan penyebut dapat dilihat pada cara di bawah.
  \[ \lim_{x \rightarrow 0} \frac{\frac{1}{x + 2} - \frac{1}{2}}{x} = \lim_{x \rightarrow 0} \left( \frac{2}{2} \right) \frac{\frac{1}{x + 2} - \frac{1}{2} \left( \frac{x + 2}{x + 2} \right) }{x} \]
  \[ = \lim_{x \rightarrow 0} \frac{\frac{2 - x - 2}{2 \left(x + 2 \right)}}{x} \]
  \[ = \lim_{x \rightarrow 0} \frac{\frac{-x}{2 \left(x + 2 \right)}}{x} \]
  \[ = \lim_{x \rightarrow 0} \frac{-x}{2 \left(x + 2 \right)} \cdot \frac{1}{x} \]
  \[ = \lim_{x \rightarrow 0} \frac{-1}{2 \left(x + 2 \right)}\]
  \[ = \frac{-1}{2 \left(0 + 2 \right)} \]
  \[ = - \frac{1}{4} \]
     4. Menyederhanakan Bentuk Aljabar
Metode atau tips ke empat dalam mencari nilai limit adalah membuka tanda kurung kemudian menyederhanakan bentuknya dan menemukan nilai limitnya. Cara ini dapat digunakan untuk mencari nilai limit dengan bentuk seperti di bawah.
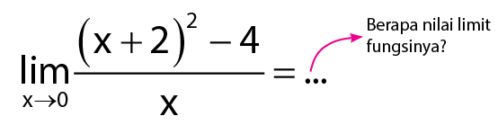
nilai imit fungsi
Hasil substitusi x pada bentuk nilai limit ini tidak menghasilkan nilai limit yang diharapkan, karena menghasilkan nilai \frac{0}{0}. Seperti terlihat pada cara di bawah.
  \[ \lim_{x \rightarrow 0} \frac{\left( x + 2 \right)^{2} - 4}{x} = \frac{\left( 0 + 2 \right)^{2} - 4}{0} \]
  \[ = \frac{2^{2} - 4}{0} \]
  \[ = \frac{4 - 4}{0} \]
  \[ = \frac{0}{0} \]
Bentuk limit yang diberikan di atas tidak dapat difaktorkan secara lebih sederhana. Sedangkan metode mengalikan dengan penyebut yang sama juga tidak dapat dilakukan karena tidak ada penyebut sama yang perlu dilakukan. Sehingga, cara menentukan bentuk limit ini adalah dengan membuka tanda kurung dan menyederhanakan bentuk aljabarnya, kemudian menemukan nilai limitnya. Cara menentukan nilai limit bentuk ini dapat dilihat pada cara di bawah.
  \[ \lim_{x \rightarrow 0} \frac{\left( x + 2 \right)^{2} - 4 }{x} \]
  \[ = \lim_{x \rightarrow 0} \frac{x^{2} + 4x + 4- 4 }{x} \]
  \[ = \lim_{x \rightarrow 0} \frac{x^{2} + 4x}{x} \]
  \[ = \lim_{x \rightarrow 0} \frac{x \left( x + 4 \right)}{x} \]
  \[ = \lim_{x \rightarrow 0} x + 4 \]
  \[ = 0 + 4 \]
  \[ = 4 \]
5. Mengalikan Akar sekawan (conjugate)
Tips menentukan nilai limit ke lima yang akan diulas adalah bentuk limit fungsi yang memiliki akar pada pembilangnya. Contoh bentuk soal yang diselesaikan dengan cara metode ini adalah seperti berikut.
Seperti biasa, kita akan menyelidiki cara menentukan limit dengan cara substitusi, pemfaktoran, dan pembilang yang sama terlebih dahulu.
Pertama, akan diselidiki cara menentukan nilai limit menggunakan metode substitusi.
  \[ \lim_{x \rightarrow 8} \frac{\sqrt{x + 1} - 3}{x - 8} = \frac{\sqrt{8 + 1} - 3}{8 - 8} \]
  \[ = \frac{\sqrt{9} - 3}{8 - 8} \]
  \[ = \frac{3 - 3}{0}\]
  \[ = \frac{0}{0} \]
Hasil yang diperoleh dengan cara di atas tidak sesuai harapan, sehingga perlu dicari menggunakan metode lain.
Metode pemfaktoran tidak dapat digunakan karena bentuk soal yang diberikan tidak dapat difaktorkan menjadi lebih sederhana lagi. Sedangkan metode dengan mengalikan pembilang juga tidak dapat dilakukan karena tidak sesuai bentuk yang diharapkan.
Sehingga, perlu cara lain yang dapat digunakan untuk menentukan nilai limitnya. Cara tersebut adalah dengan merasionalkannya. Untuk lebih jeasnya, perhatikan cara menentukan limit yang akan diberikan pada ulasan di bawah.
  \[ \lim_{x \rightarrow 8} \frac{\sqrt{x + 1} - 3}{x - 8} = \lim_{x \rightarrow 8} \frac{\sqrt{x + 1} - 3}{x - 8} \cdot \frac{\sqrt{x + 1} + 3}{\sqrt{x + 1} + 3} \]
  \[ = \lim_{x \rightarrow 8} \frac{ \left( x + 1 \right) - 3\sqrt{x + 1} + 3\sqrt{x + 1} - 9}{\left(x - 8 \right) \left( \sqrt{x + 1} + 3 \right) } \]
  \[ = \lim_{x \rightarrow 8} \frac{ \left( x - 8 \right)}{\left(x - 8 \right) \left( \sqrt{x + 1} + 3 \right)} \]
  \[ = \lim_{x \rightarrow 8} \frac{1}{ \left( \sqrt{x + 1} + 3 \right) } \]
  \[ = \frac{1}{ \left( \sqrt{8 + 1} + 3 \right) } \]
  \[ = \frac{1}{ \left( \sqrt{9} + 3 \right) } \]
  \[ = \frac{1}{ \left( 3 + 3 \right) } \]
  \[ = \frac{1}{6} \]
Kita mendapatkan hasil nilai limit fungsi sesuai harapan.
     6. Bentuk limit \frac{sin \; x}{x}
Bentuk limit lainnya adalah bentuk limit fungsi yang mengandung persamaan \frac{sin \; x}{x} = 1. Sebelum mempelajari lebih jauh tentang bentuk limit fungsi yang memiliki bentuk \frac{sin \; x}{x} = 1, simak persamaan limit fungsi berikut :
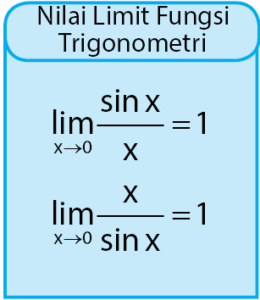
Limit fungsi trigonometri
Persamaan di atas dapat digunakan untuk menyelesaikan bentuk limit yang mengandung bentuk \frac{sin \; x}{x} seperti contoh soal yang diberikan di bawah.
  \[ \lim_{x \rightarrow 0} \frac{sin \; 2x}{x} \]
Cara mengerjakannya adalah :
  \[ lim_{x \rightarrow 0} \frac{sin \; 2x}{x} = lim_{x \rightarrow 0} \frac{sin \; 2x}{ 2x} \cdot \frac{2}{1} \]
  \[ = 1 \cdot \frac{2}{1} = 2 \]
Nilai limit yang diharapkan. Contoh lain akan diberikan seperti di bawah.
  \[ \lim_{x \rightarrow 0} \frac{x + sin \; x}{x} = \lim_{x \rightarrow 0} \frac{x}{x} + \frac{sin \; x}{x} \]
  \[ = \lim_{x \rightarrow 0} \left( 1 + \frac{sin \; x}{x} \right) \]
  \[ = \lim_{x \rightarrow 0} 1 + \lim_{x \rightarrow 0} \frac{sin \; x}{x} \]
  \[ = 1 + 1 = 2 \]
Contoh lain:
  \[ \lim_{x \rightarrow 0} \frac{4 \cdot sin \; 5x}{sin \; 4x} = \lim_{x \rightarrow 0} \frac{4x \cdot sin \; 5x}{sin \; 4x} \]
  \[ = \lim_{x \rightarrow 0} \frac{4x \cdot sin \; 5x}{sin \; 4x \cdot 5x} \cdot \frac{5x}{x} \]
  \[ = \lim_{x \rightarrow 0} \frac{4x}{sin \; 4x} \cdot \frac{sin \; 5x}{5x} \cdot \frac{5x}{x} \]
  \[ = 1 \cdot 1 \cdot 5 \]
  \[ = 5 \]
7. Bentuk Limit Nilai Mutlak
Tips terakhir yang akan diulas pada halaman ini adalah cara menentukan nilai imit fungsi bentuk nilai mutlak. Sebelumnya pahami dulu cara menentukan nilai mutlak yang akan diberikan di bawah.
nilsi mutlak
Berdasarkan persamaan di atas, kesimpulannya adalah nilai mutlak x akan bernilai x jika x \geq 0 dan nilai mutlak x akan bernilai -x jika x < 0. Selanjutnya, kita akan masuk dalam ulasan materi mencari nilai limit fungsi nilai mutak. Perhatikan persamaan di bawah.
  \[ \lim_{x \rightarrow 2} \frac{\left| x - 2\right|}{x - 2} \]
Berdasarkan cara mencari nilai mutlak, akan diperoleh persamaan sebagai berikut.
  \[ \left| x - 2 \right| = x - 2, \; x >= 2 \]
  \[ \left| x - 2 \right| = -(x - 2), \; x < 2 \]

 Nilai limit dari kanan:
  \[ \lim_{x \rightarrow 2^{+}} \frac{x - 2}{x - 2} = 1 \]

 Nilai limit dari kiri:
  \[ \lim_{x \rightarrow 2^{-}} \frac{-(x - 2)}{x - 2} = - 1 \]
Nilai limit dari kanan tidak sama dengan nilai limit dari kiri, sehingga kesimpulannya adalah nilai limit tidak ada. Nilai limit hanya diperoleh ketika nilai limit dari kanan sama dengan nilai limit dari kiri.
Jika disajikan dalam gambar akan terlihat seperti berikut.
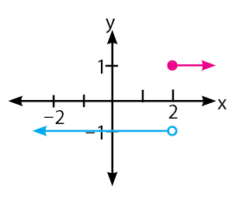
grafik nilai mutlak
Terlihat bahwa fungsi membentuk garis yang tidak terhubung (diskontinu).
Diposting oleh di

Tidak ada komentar:

Posting Komentar

Langganan: Posting Komentar (Atom)